Complex Waveforms I - Fourier Series
As has been known since ancient times, a vibrating string produces a set of harmonics, tones that are integer multiples of the fundamental pitch. Today, we know that any complex waveform made up of harmonics can be produced by a sum of sine and cosine waves, as shown by the Fourier theorem.
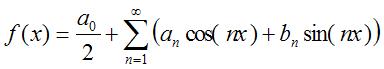
In plain language, the Fourier series produces a periodic waveform from a sum of cosine and sine waves. The first term, a0/2 is the center amplitude and can be set to 0 for audio signals. We can represent a sum of sine and cosine as either a sine or cosine with the appropriate amplitude and phase offset. Thus, an easy way to produce more complex waveforms is to sum together sine waves of different frequencies, amplitudes and initial phase. We can’t produce an infinite series of sine waves, so we have to limit the summation to some reasonable number. That leaves us with:
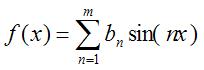
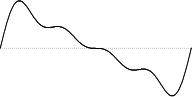
The following code sums the first four partials to produce a waveform with the shape of a "wiggly" ramp. Each partial has an amplitude that is the inverse of its number, such that higher frequencies have less amplitude. Because we are adding multiple waveforms, we need to rescale the sum to keep the value in the range [-1,+1].
phsIncr = twoPI / sampleRate * frequency;
phase = 0;
scale = 1.58;
for (n = 0; n < totalSamples; n++) {
value = 0;
for (p = 1; p <= 4; p++)
value += sin(phase*p) / p;
if ((phase += phsIncr) >= twoPI)
phase -= twoPI;
sample[n] = value / scale;
}
The resulting waveform looks like this:
In this example, the multiple and amplitude of each partial is fixed. For a more useful program, we can store the multiples and amplitudes of the partials in separate arrays. We can also convert the multiplication of the fundamental phase into separate summations for each partial. We can set the initial phase of each partial, and/or change the sign of the amplitude, to represent a cosine value.
A potential problem with summing sine waves is that multiples of the fundamental frequency can exceed the Nyquist limit. To prevent that from happening, we can test each partial against the Nyquist limit and eliminate any partials that would create a problem. A more optimal algorithm is to test each phase increment as it is calculated and reduce the count of partials accordingly. This prevents excess code execution inside the generator loop.
The Waveform Investigator
The Waveform Investigator is a utility program that demonstrates the effect of summing harmonic frequencies at different amplitudes. As such, it implements a simple Fourier series synthesis method. The waveforms created by this method can be stored in a table and used by a wavetable oscillator.
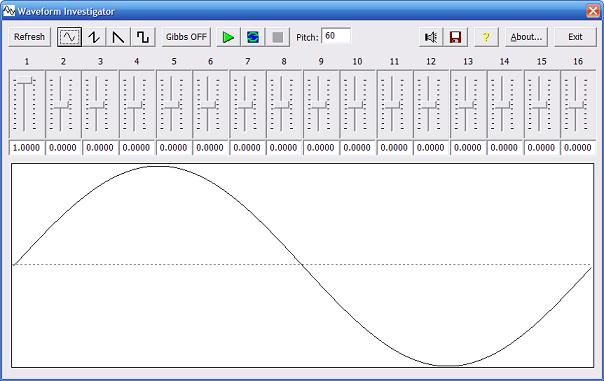
The amplitude of each partial is set with the sliders or edit fields. The amplitude ranges from 0-1. Changing a slider automatically updates the edit field. Entering a value in the edit field will update the slider on exit from the edit field. Changes to the amplitude values will update the waveform plot when one of the top row function buttons is pressed.
Refresh - this button will update the plot with the current values.
Preset Waveforms - The four preset waveform buttons will set the amplitudes of the partials to produce the indicated waveform.
Gibbs On/Off - When "ON" this will adjust the amplitude values for the "Gibbs phenonmen" by applying the Lanczos sigma value to the amplitude of all partias > 1.
To hear the waveform, press the Play (>) button or Loop () button. The play button will play two seconds of the sound. The Loop button will repeat the sound until the Stop [] button is pressed.
The pitch entry field can be used to change the pitch. Pitch is specified with an integer value 0-120 with Middle C at 60 (ala MIDI).
The "loudspeaker" button will save the sound to a .WAV file. The "disk" button will save the plot to a metafile (.EMF) that can be displayed in a word processor or graphics program.